Variables aléatoires à densité (Appro)
Généralités
Quand dit-on qu’une variable aléatoire est à densité ?
On appelle variable aléatoire à densité toute variable aléatoire \( X \) dont la fonction de répartition \( F_X \) est continue sur \( \mathbb{R}\) et de classe \( \mathcal{C}^1 \) sur \( \mathbb{R} \) éventuellement privé d’un ensemble fini de points.
Propriétés de la fonction de répartition d’une variable aléatoire à densité
Soit \(F\) une fonction définie sur \(\mathbb{R}\), à valeurs dans \(\mathbb{R}\). \(F\) est la fonction de répartition d’une variable aléatoire à densité si et seulement si :
- \( F \) est continue sur \(\mathbb{R}\),
- \(F\) est de classe \(\mathcal{C}^1\) sur \(\mathbb{R}\), éventuellement privé d’un ensemble fini de points,
- \(F\) est croissante sur \(\mathbb{R}\),
- \( \displaystyle \lim _{x \rightarrow-\infty} F(x)=0\) et \( \displaystyle \lim _{x \rightarrow+\infty} F(x)=1\).
Densité de probabilité : définition et propriétés
Définition
Si \(X\) est une variable aléatoire à densité de fonction de répartition \(F_X\), on appelle densité de \(X\) toute fonction \(f_X\) définie et positive sur \(\mathbb{R}\) et telle que \(f_X(x)=F_X^{\prime}(x)\) pour tout \(x\) appartenant à \(\mathbb{R}\) éventuellement privé d’un ensemble fini de points.
Propriétés
Soit \(f\) une fonction définie sur \(\mathbb{R}\) et à valeurs dans \(\mathbb{R}\). \(f\) est une densité de probabilité si et seulement si : \(f\) est positive sur \(\mathbb{R}\), \(f\) est continue sur \(\mathbb{R}\) éventuellement privé d’un ensemble fini de points, \(\displaystyle \int_{-\infty}^{+\infty} f(t) \, \mathrm{d} t\) converge et : \( \displaystyle \int_{-\infty}^{+\infty} f(t) \, \mathrm{d} t=1\).
Lien entre densité et fonction de répartition d’une variable aléatoire à densité
Si \(X\) est une variable aléatoire à densité, de fonction de répartition \(F_X\) et de densité \(f_X\), alors :
- \( \forall x \in \mathbb{R}, \ \displaystyle \mathbb{P}(X \leqslant x)=\mathbb{P}(X<x)=F_X(x)=\int_{-\infty}^x f_X(t) \, \mathrm{d} t\),
- \( \forall x \in \mathbb{R}, \ \displaystyle \mathbb{P}(X>x)=\mathbb{P}(X \geqslant x)=1-F_X(x)=\int_x^{+\infty} f_X(t) \, \mathrm{d} t\),
- \( \displaystyle \forall(a, b) \in \mathbb{R}^2 \ / \ a<b, \ \mathbb{P}(a<X \leqslant b)=F_X(b)-F_X(a)=\int_a^b f_X(t) \, \mathrm{d} t\),
- \( f_x(x)=F_X^{\prime}(x) \) pour tout réel \( x\) en lequel \( f_X \) est continue.
Moments d’une variable aléatoire à densité
Espérance d’une variable aléatoire à densité : définition et propriétés
Définition
Soit \(X\) une variable aléatoire à densité, de densité \(f_X\).
On dit que \(X\) admet une espérance si l’intégrale \( \displaystyle \int_{-\infty}^{+\infty} t \,f_X(t) \, \mathrm{d} t\) est absolument convergente. Dans ce cas, l’espérance de \(X\), notée \(\mathbb{E}(X)\), est définie par : \[ \mathbb{E}(X)=\int_{-\infty}^{+\infty} t \, f_X(t) \, \mathrm{d} t \]
Lorsque l’espérance de \(X\) est nulle, on dit que \(X\) est une variable aléatoire centrée.
Propriétés
Soit \(X\) est une variable aléatoire admettant une espérance.
- Si \(X\) est une variable aléatoire positive, alors : \(\mathbb{E}(X) \geqslant 0\) (positivité de l’espérance),
- Pour tout couple \((a, b)\) de réels, \(a X+b\) admet une espérance et : \( \mathbb{E}(a X+b)=a \mathbb{E}(X)+b \) (linéarité de l’espérance).
Théorème de transfert
Soit \(X\) une variable aléatoire à densité, de densité \(f_X\). On suppose que \(X(\Omega)\) est un intervalle d’extrémités \(a\) et \(b\) telles que \(-\infty \leqslant a<b \leqslant+\infty\).
Si \(\varphi\) est une fonction définie sur \(X(\Omega)\) et continue sur \(X(\Omega)\) éventuellement privé d’un ensemble fini, alors \(Y=\varphi \circ X\) admet une espérance si et seulement si l’intégrale \( \displaystyle \int_a^b \varphi(t) \, f_X(t) \, \mathrm{d} t\) est absolument convergente et, dans ce cas : \[ \mathbb{E}(\varphi(X))=\int_a^b \varphi(t) \, f_X(t) \, \mathrm{d} t \]
Moments d’une variable aléatoire à densité : définition
Soit \(X\) une variable aléatoire à densité, de densité \(f_X\) et \(r \in \mathbb{N}^*\).
On dit que \(X\) admet un moment d’ordre \( r \) si \(X^r\) admet une espérance (c’est-à-dire, d’après le théorème de transfert, si l’intégrale \( \displaystyle \int_{-\infty}^{+\infty} t^r f_X(t) \, \mathrm{d} t\) est absolument convergente).
Dans ce cas le moment d’ordre \(r\), noté \(m_r(X)\) est défini par : \[ m_r(X)=\mathbb{E}\left(X^r\right)=\int_{-\infty}^{+\infty} t^r f_X(t) \, \mathrm{d} t \]
Variance d’une variable aléatoire à densité : définition et propriétés
Définition
Soit \(X\) une variable aléatoire à densité, de densité \(f_X\).
- On dit que \(X\) admet une variance si \(X\) admet une espérance et si \(X-\mathbb{E}(X)\) admet un moment d’ordre 2. Dans ce cas, la variance de \(X\), notée \(\mathbb{V}(X)\), est définie par : \[ \mathbb{V}(X)=\mathbb{E} ((X-\mathbb{E}(X))^2 )=\int_{-\infty}^{+\infty}(t-\mathbb{E}(X))^2 f_X(t) \, \mathrm{d} t \]
- Si \(X\) admet une variance, on appelle écart-type de \(X\) le réel \(\sigma(X)\) défini par : \[ \sigma(X)=\sqrt{\mathbb{V}(X)} \]
- Lorsque la variance de \(X\) est égale à \( 1 \), on dit que \(X\) est une variable aléatoire réduite.
Propriétés
Soit \(X\) une variable aléatoire à densité.
- \(X\) admet une variance si et seulement si \(X\) admet un moment d’ordre 2.
- Formule de Koenig-Huygens. Si \(X\) admet une variance, alors :\[ \mathbb{V}(X)=\mathbb{E}\left(X^2\right)-[\mathbb{E}(X)]^2 \]
- Si \(X\) admet une variance, alors, pour tout \((a, b) \in \mathbb{R}^2, a X+b\) admet une variance et : \[ \mathbb{V}(a X+b)=a^2 \mathbb{V}(X) \]
Lois usuelles
Loi uniforme : définition et propriétés
Soit \( a \) et \( b \) deux réels tels que \( a < b \).
Densité
On dit que \(X\) suit la loi uniforme sur \([a, b]\) (notée \(\mathcal{U}([a, b]))\) si elle admet pour densité la fonction \(f\) définie par : \[ \forall x \in \mathbb{R}, \ f(x)=\frac{1}{b-a} \, \mathbb{1}_{[a, b]}(x)= \begin{cases} \dfrac{1}{b-a} & \text { si } x \in[a, b] \\ \hfill 0 \hfill & \text { sinon } \end{cases} \]
Fonction de répartition
Si \(X\) suit la loi uniforme sur \([a, b]\), alors sa fonction de répartition est définie par : \[ \forall x \in \mathbb{R}, \ \mathbb{P}(X \leqslant x)= \begin{cases} \hfill 0\hfill & \text { si } x<a \\ \hfill \dfrac{x-a}{b-a} \hfill & \text { si } x \in[a, b] \\ \hfill 1 \hfill & \text { si } x>b \end{cases} \]
Espérance et variance
Si \(X\) suit la loi uniforme sur \([a, b], X\) admet une espérance et une variance et : \[ \mathbb{E}(X)=\frac{a+b}{2} \quad \text { et } \quad \mathbb{V}(X)=\frac{(b-a)^2}{12} \]
Lien entre lois \( \mathcal{U}([0,1]) \) et \( \mathcal{U}([a, b]) \)
Si \(X\) est une variable aléatoire alors : \[ X \hookrightarrow \mathcal{U}([0,1]) \Leftrightarrow a+ \left( b-a \right) X \hookrightarrow \mathcal{U}([a, b]) \]
Loi exponentielle : définition et propriétés
Soit \(\lambda \) un réel strictement positif.
Densité
On dit que \(X\) suit la loi exponentielle de paramètre \(\lambda \) (notée \(\mathcal{E}(\lambda)\) ) si elle admet pour densité la fonction \(f\) définie par : \[ \forall x \in \mathbb{R}, \ f(x)=\lambda \, \mathrm{e}^{-\lambda x} \, \mathbb{1}_{\mathbb{R}^{+}}(x)= \begin{cases} \lambda \mathrm{e}^{-\lambda x} & \text { si } x \geqslant 0 \\ \hfill 0 \hfill & \text { sinon } \end{cases} \]
Fonction de répartition
Si \(X\) suit la loi exponentielle de paramètre \(\lambda\), alors sa fonction de répartition est définie par : \[ \forall x \in \mathbb{R}, \ \mathbb{P}(X \leqslant x)= \begin{cases} \hfill 0 \hfill & \text { si } x<0 \\ 1-\mathrm{e}^{-\lambda x} & \text { si } x \geqslant 0 \end{cases} \]
Espérance et variance
Si \(X\) suit la loi exponentielle de paramètre \(\lambda\), \( X\) admet une espérance et une variance et : \[ \mathbb{E}(X)=\frac{1}{\lambda} \quad \text { et } \quad \mathbb{V}(X)=\frac{1}{\lambda^2} \]
Lien entre lois \( \mathcal{E}(1) \) et \( \mathcal{E}(\lambda) \)
Si \(X\) est une variable aléatoire alors : \[ X \hookrightarrow \mathcal{E}(1) \Leftrightarrow \frac{1}{\lambda} X \hookrightarrow \mathcal{E}(\lambda) \]
Absence de mémoire
Soit \(X\) une variable aléatoire à densité, à valeurs dans \(\mathbb{R}^{+}\) et telle que : \[\forall x \in \mathbb{R}_{+}^*, \ \mathbb{P}(X>x) \neq 0 \] \(X\) suit la loi exponentielle si et seulement si sa loi est sans mémoire, c’est-à-dire si et seulement si : \[ \forall(x, y) \in\left(\mathbb{R}_{+}^*\right)^2, \ \mathbb{P}_{[X>x]}(X>x+y)=\mathbb{P}(X>y) \]
Loi normale : définition et propriétés
Soit \( m \) un réel et \( \sigma \) un réel strictement positif.
Densité
On dit que \(X\) suit la loi normale de paramètre \(m \) et \(\sigma^2\), notée \(\mathcal{N}\left(m, \sigma^2\right)\), si elle admet pour densité la fonction \(\varphi\) définie par : \[ \forall x \in \mathbb{R}, \ \varphi(x)=\frac{1}{\sqrt{2 \pi \sigma^2}} \, \mathrm{e}^{-\frac{(x-m)^2}{2 \sigma^2}} \]
Espérance et variance
Si \(X\) suit la loi normale de paramètres \(m\) et \(\sigma^2\), \( X\) admet une espérance et une variance et : \[ \mathbb{E}(X)=m \quad \text { et } \quad \mathbb{V}(X)=\sigma^2 \]
En particulier, si \(X\) suit la loi normale \(\mathcal{N}(0,1), X\) est centrée et réduite; dans ce cas, on dit donc que \(X\) suit la loi normale centrée réduite.
Lien entre les lois \( \mathcal{N}(0,1) \) et \( \mathcal{N}(m, \sigma^2) \)
Si \(X\) est une variable aléatoire : \[ X \hookrightarrow \mathcal{N}(0,1) \Leftrightarrow \sigma X+m \hookrightarrow \mathcal{N}(m, \sigma^2) \]
Éléments de symétrie du graphe de la fonction de répartition de la loi normale centrée réduite. Allure du graphe
Soit \(X\) une variable aléatoire suivant la loi normale centrée réduite. En notant \(\Phi\) sa fonction de répartition, on a : \[ \forall x \in \mathbb{R}, \Phi(-x)=1-\Phi(x) \] Ainsi la courbe représentative de \(\Phi\) dans un repère orthonormé admet pour centre de symétrie le point de coordonnées \(\left(0, \frac{1}{2}\right)\). L’allure de la courbe représentative de \(\Phi\) est la suivante :
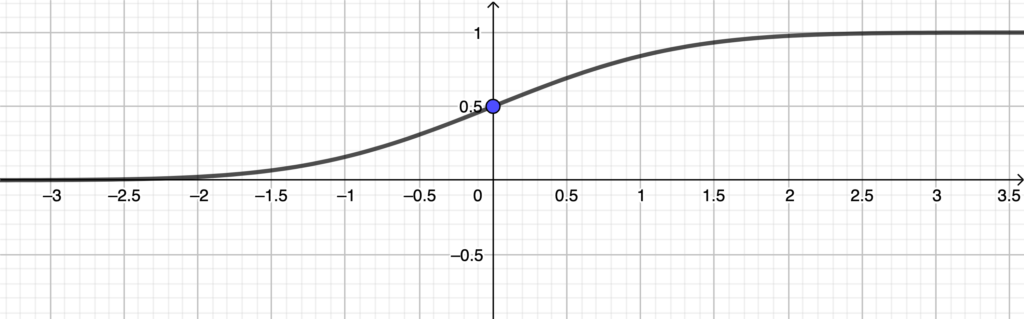
Graphe de la densité usuelle d’une loi normale
Le graphe de la fonction \( \displaystyle \varphi: x \mapsto \frac{1}{\sqrt{2 \pi \sigma^2}} \, \mathrm{e}^{-\frac{(x-m)^2}{2 \sigma^2}}\) est une “courbe en cloche” qui admet : –
- un axe de symétrie : la droite d’équation \(x=m\),
- deux points d’inflexion : les points d’abscisses respectives \(m-\sigma\) et \(m+\sigma\).
Par exemple, pour \(m=2\) et \(\sigma=3\), le graphe de cette fonction est le suivant :
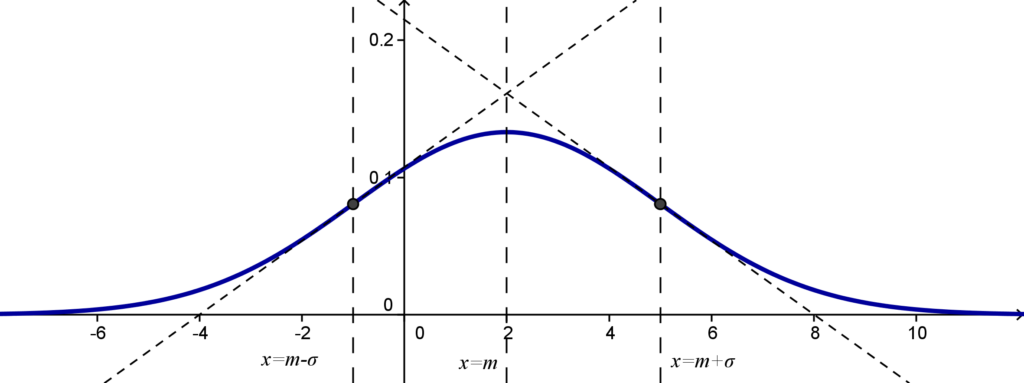
Loi gamma : définition et propriétés
Soit \( \nu \) un réel strictement positif.
Densité
On dit que \(X\) suit la loi gamma de paramètre \(\nu\) (notée \(\gamma(\nu)\)) si elle admet pour densité la fonction \(f\) définie par : \[ \forall x \in \mathbb{R}, \ f(x)=\frac{1}{\Gamma(\nu)} \, x^{\nu-1} \, \mathrm{e}^{-x} \, \mathbb{1}_{\mathbb{R}_{+}^*}(x)= \begin{cases} \dfrac{1}{\Gamma(\nu)} \, x^{\nu-1}\, \mathrm{e}^{-x} & \text { si } x>0 \\ \hfill 0 \hfill & \text { sinon } \end{cases} \]
Espérance et variance
Si \(X\) suit la loi gamma de paramètre \(\nu \), \( X\) admet une espérance et une variance et : \[ \mathbb{E}(X)=\mathbb{V}(X)=\nu \]
Sommes de variables aléatoires à densité indépendantes
Loi de la somme de variables aléatoires à densité indépendantes
Produit de convolution
Soit \(f\) et \(g\) deux densité de probabilité.
On appelle produit de convolution de \(f\) et \(g\) la fonction \(h=f \star g\) définie (sous réserve de convergence) par : \[ \forall x \in \mathbb{R}, \ h(x)=(f \star g)(x)=\int_{-\infty}^{+\infty} f(t) \, g(x-t) \, \mathrm{d} t=\int_{-\infty}^{+\infty} f(x-t) \, g(t) \, \mathrm{d} t \]
Si \(f\) ou \(f\) est bornée, alors \(f \star g\) est une fonction définie sur \(\mathbb{R}\), continue sur \(\mathbb{R}\) éventuellement privé d’un ensemble fini.
Théorème de convolution
Soit \(X\) et \(Y\) deux variables aléatoires à densité indépendantes, \(f_X\) une densité de \(X\) et \(f_Y\) une densité de \(Y\).
Si le produit de convolution \(f_X \star f_Y\) est une fonction définie sur \(\mathbb{R}\), continue sur \(\mathbb{R}\) éventuellement privé d’un ensemble fini, alors \(X+Y\) est une variable aléatoire à densité dont une densité est \(f_{X+Y}=f_X \star f_Y\), c’est-à-dire : \[ \forall x \in \mathbb{R}, \ f_{X+Y}(x)=\int_{-\infty}^{+\infty} f_X(t) \, f_Y(x-t) \, \mathrm{d} t=\int_{-\infty}^{+\infty} f_X(x-t) \, f_Y(t) \, \mathrm{d} t \]
Loi de la somme de variable aléatoires indépendantes suivant des lois normales
- Si \(X\) et \(Y\) sont deux variables aléatoires indépendantes suivant respectivement les lois \(\mathcal{N}(m_1, \sigma_1^2)\) et \(\mathcal{N}(m_2, \sigma_2^2)\), alors \(X+Y\) suit la loi normale \(\mathcal{N}(m_1+m_2, \sigma_1^2+\sigma_2^2)\).
- Plus généralement, si \(X_1, \ldots, X_n\) sont \(n\) variables aléatoires indépendantes suivant respectivement les lois \(\mathcal{N}(m_1, \sigma_1^2), \ldots, \mathcal{N}(m_n, \sigma_n^2)\), alors \(X_1+\cdots+X_n\) suit la loi \(\mathcal{N}(m_1+\cdots m_n, \sigma_1^2+\cdots+\sigma_n^2)\).
Loi de la somme de variable aléatoires indépendantes suivant des lois gamma
- Si \(X\) et \(Y\) sont deux variables aléatoires indépendantes suivant respectivement les lois \(\gamma(\nu_1)\) et \(\gamma(\nu_2)\), alors \(X+Y\) suit la loi \(\gamma(\nu_1+\nu_2)\).
- Plus généralement, si \(X_1, \ldots, X_n\) sont \(n\) variables aléatoires indépendantes suivant respectivement les lois \(\gamma(\nu_1), \ldots, \gamma(\nu_n)\), alors \(X_1+\cdots+X_n\) suit la loi \(\gamma(\nu_1+\cdots+\nu_n)\).
Loi de la somme de variable aléatoires indépendantes suivant des lois exponentielles de paramètre \( 1 \)
Si \(X_1, \ldots, X_n\) sont \(n\) variables aléatoires indépendantes suivant toutes la même loi exponentielle \(\mathcal{E}(1)\), alors \(X_1+\cdots+X_n\) suit la loi \(\gamma(n)\).
