Fonctions : convexité
Dans tout ce chapitre, \( f \) désigne une fonction définie sur un intervalle \( I \) de \( \mathbb{R} \) et à valeurs dans \( \mathbb{R} \).
Fonction convexe, concave : définition et interprétation graphique
Définitions
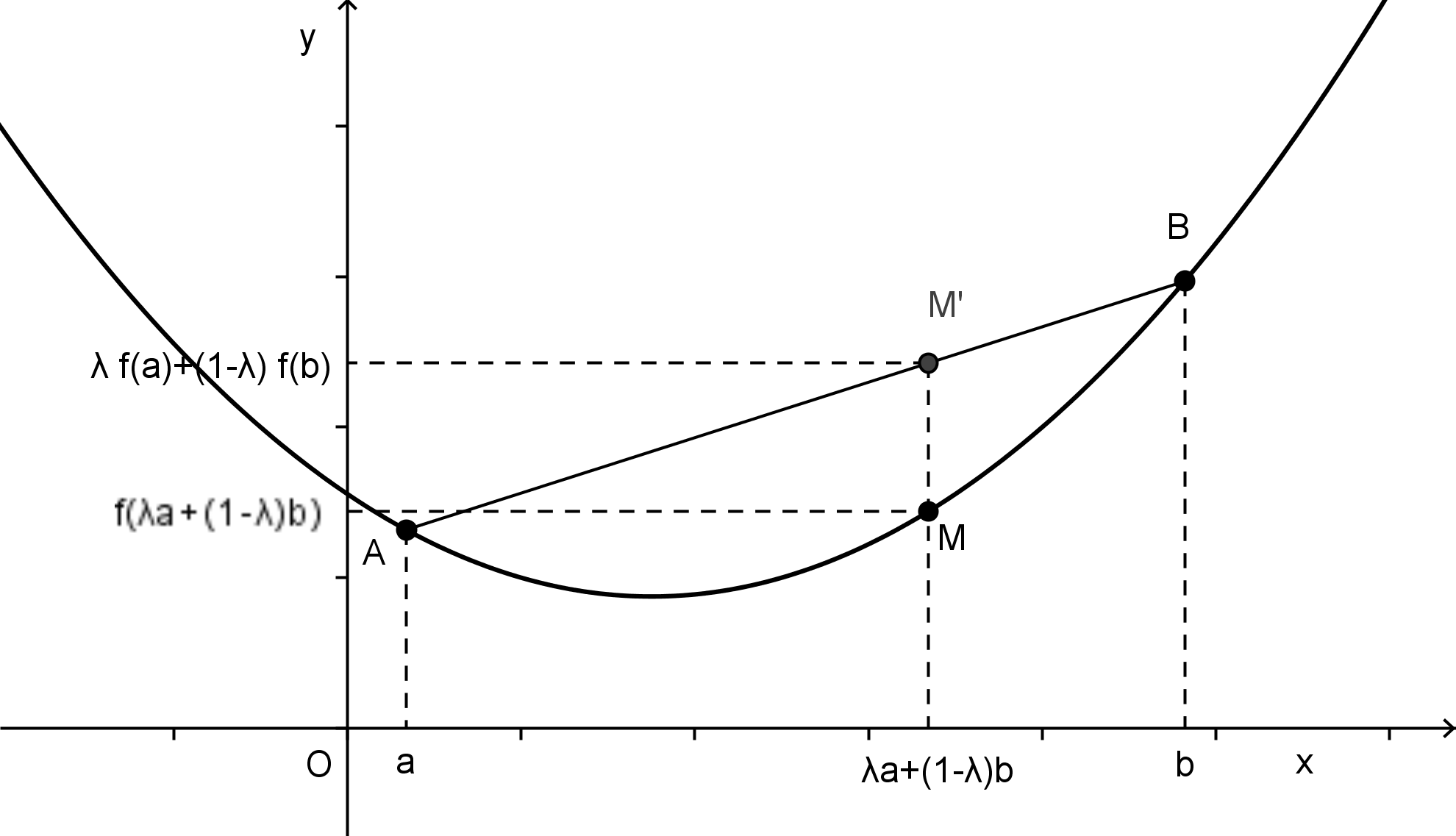
- On dit que \(f\) est convexe sur \(I\) si : \[ \forall(x, y) \in I^2, \ \forall \lambda \in[0,1], \ f(\lambda x+(1-\lambda) y) \leqslant \lambda f(x)+(1-\lambda) f(y) \]
- On dit que \(f\) est concave sur \(I\) si \(-f\) est convexe sur \(I\), c’est-à-dire si : \[ \forall(x, y) \in I^2, \ \forall \lambda \in[0,1], \ f(\lambda x+(1-\lambda) y) \geqslant \lambda f(x)+(1-\lambda) f(y) \]
- Si \(a\) est un élément de \(\stackrel{\circ}{I}\), on dit que le point de coordonnées \((a, f(a)\) ) est un point d’inflexion de \(f\) s’il existe un réel \(\alpha\) strictement positif tel que l’intervalle \(] a-\alpha, a+\alpha[\) soit inclus dans \(I\) et tel que \(f\) soit convexe sur \(] a-\alpha, a]\) et concave sur \([a, a+\alpha[\) ou tel que \(f\) est concave sur \(] a-\alpha, a]\) et convexe sur \([a, a+\alpha[\).
Interprétation graphique
Une fonction convexe est une fonction dont le graphe est en dessous de ses cordes et une fonction concave est une fonction dont le graphe est au dessus de ses cordes.
Inégalité de Jensen (appro)
Soit \(f\) une fonction convexe sur un intervalle \(I\) de \(\mathbb{R}\). Pour tout \(n \in \mathbb{N}^*\), pour tout \(\left(x_1, \ldots, x_n\right) \in I^n\) et pour tout \(\left(\lambda_1, \ldots, \lambda_n\right) \in\left(\mathbb{R}^{+}\right)^n\) tel que \(\sum_{k=1}^n \lambda_k=1\), on a : \[ f \! \left(\sum_{k=1}^n \lambda_k x_k\right) \leqslant \sum_{k=1}^n \lambda_k f (x_k ) \]
Caractérisation des fonctions convexes de classe \( \mathcal{C}^1 \)
Les assertions suivantes sont équivalentes :
- \(f\) est convexe sur \(I\),
- \(f^{\prime}\) est croissante sur \(I\),
- la courbe représentative de \(f\) est “au dessus” de toutes ses tangentes.
Caractérisation des fonctions convexes de classe \( \mathcal{C}^2 \)
Si \(f\) est de classe \(\mathcal{C}^2\) sur \(I\), \(f\) est convexe sur \(I\) si et seulement si \(f^{\prime \prime}\) est positive ou nulle sur \(I\).
