15 minutes de Python
Représentation graphique : utiliser la fonction plt.plot
Tracer une courbe avec plt.plot
Le module matplotlib.pyplot permet de représenter graphiquement des données.
Dans ce chapitre, on utilise essentiellement la fonction plt.plot pour tracer
une courbe à partir d’une liste (ou d’un tableau numpy) d’abscisses et d’ordonnées.
import matplotlib.pyplot as pltLa commande la plus utilisée est :
plt.plot(x,y)
où x et y sont deux listes (ou tableaux numpy) de même longueur.
Si l’on note \(x = (x_0,\dots,x_n)\) et \(y = (y_0,\dots,y_n)\), la commande
plt.plot(x,y) représente les points \((x_0,y_0), (x_1,y_1), \dots, (x_n,y_n)\) ;
ces points sont ensuite reliés dans l’ordre par des segments, ce qui permet d’obtenir
une ligne brisée qui approche le graphe de la relation entre \(x\) et \(y\)
(en particulier le graphe d’une fonction lorsque \(y = f(x)\)).
L’ordre des points est celui dans lequel ils apparaissent dans le tableau x.
On affiche ensuite la figure avec :
plt.show()On peut préciser un style de tracé avec un troisième argument, par exemple :
plt.plot(x,y,'o'): points uniquement (représentés par le symbole « o »),plt.plot(x,y,'x'): points uniquement (représentés par le symbole « x »),plt.plot(x,y,color=‘red'): ligne de couleur rouge,plt.plot(x,y,'--'): ligne en pointillés…
On peut aussi améliorer le rendu avec quelques commandes usuelles :
plt.grid(): affiche une grille,plt.title('Titre'): ajoute un titre,plt.xlabel('x'),plt.ylabel('y'): légendes des axes,plt.legend(): affiche la légende (si l’on a utilisé l’optionlabel=...).
Représenter graphiquement une fonction
Pour tracer le graphe d’une fonction \(f\) sur un intervalle \([a,b]\), on choisit un grand nombre de points \(x\) entre \(a\) et \(b\), puis on calcule les valeurs correspondantes \(f(x)\).
On utilise pour cela np.linspace(a,b,N) qui construit un tableau de N valeurs
régulièrement espacées entre a et b.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 - 2*x + 1
x = np.linspace(-1, 3, 200)
y = f(x)
plt.plot(x, y)
plt.grid()
plt.show()Ici, on a défini la fonction \(f\) par \(f(x)=x^2-2x+1\).
L’instruction x = np.linspace(-1,3,200) construit un tableau de 200 valeurs
régulièrement espacées entre \(-1\) et \(3\).
On calcule ensuite y = f(x), ce qui fournit les valeurs \(f(x_k)\).
La commande plt.plot(x,y) trace alors les points \((x_k,f(x_k))\) reliés par des segments.
La figure affichée est donc une approximation du graphe de \(f\) sur \([-1,3]\).
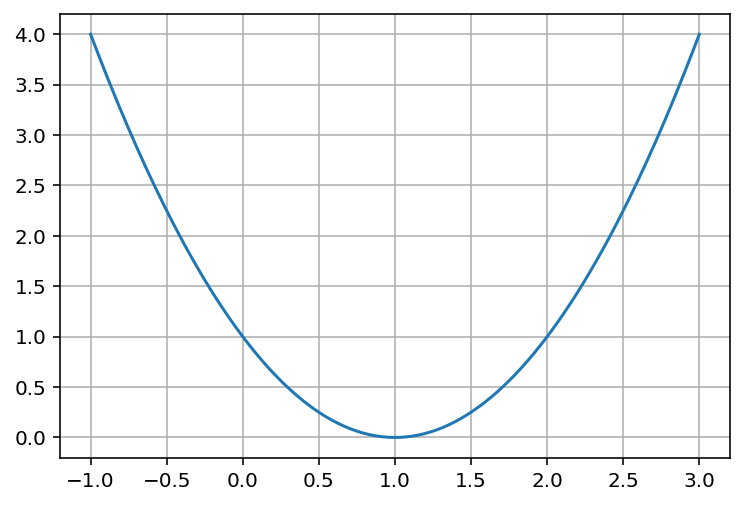
Graphe de la fonction \(f : x \mapsto (x-1)^2\) sur \([-1,3]\).
Représenter graphiquement les termes d’une suite
Pour une suite \((u_n)\), on représente souvent les points de coordonnées \((n,u_n)\) afin de visualiser le comportement de la suite (croissance, oscillations, éventuelle convergence).
On calcule d’abord les valeurs de \(u_n\) pour \(n\in\{0,\ldots,N\}\), puis on trace :
plt.plot(n, u)
où n est la liste des indices et u la liste des valeurs correspondantes.
import numpy as np
import matplotlib.pyplot as plt
N = 30
n = np.arange(N+1)
u = np.zeros(N+1)
u[0] = 5
for k in range(N):
u[k+1] = (u[k] + 2)/3
plt.plot(n, u, 'x')
plt.grid()
plt.show()On calcule ici les 30 premiers termes de la suite \((u_n)\) définie par \(u_0=5\) et par la relation de récurrence \[\forall n\in\mathbb{N},\ u_{n+1}=\dfrac{u_n+2}{3}\]
La variable n contient les indices \(0,1,\dots,N\) et le tableau u
contient les valeurs \(u_0,u_1,\dots,u_N\) calculées dans la boucle.
La commande plt.plot(n,u,’x') représente alors les points \((n,u_n)\)
(sous forme de marqueurs), ce qui permet de visualiser l’évolution de la suite
et de conjecturer une éventuelle limite.
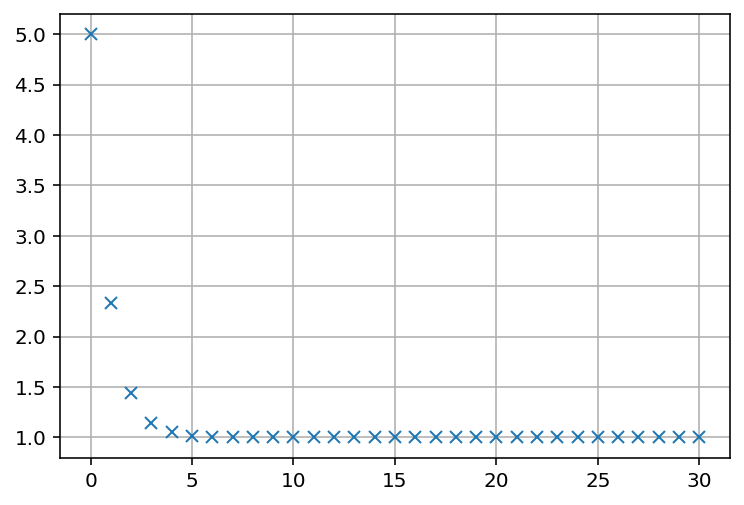
Représentation des points \((n,u_n)\) pour \(0\le n\le N\).
Exemple
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 200)
y = np.log(1 + x)
plt.plot(x, y)
plt.grid()
plt.show()Explication
La commande np.linspace(0,4,200) construit un tableau x contenant 200 valeurs
régulièrement espacées entre 0 et 4.
Puis l’instruction
y = np.log(1 + x)
calcule les valeurs de la fonction \(f\) définie par \(f(t)=\ln(1+t)\) sur ces points.
Le tableau y contient donc les valeurs \(f(x_k)\).
La commande
plt.plot(x, y)trace alors la courbe obtenue en représentant les points \((x_k,y_k)\), c’est-à-dire une approximation du graphe de la fonction \(t \mapsto \ln(1+t)\) sur \([0,4]\).
Enfin, plt.grid() affiche une grille pour faciliter la lecture,
et plt.show() affiche la figure à l’écran.
Trois commandes utiles aujourd’hui
Clique sur une carte pour voir l’instruction utile.
np.arange(a, b, h)
Renvoie un tableau contenant les valeurs a, a+h, a+2h, … strictement inférieures à b.
np.linspace(a, b, n)
Renvoie un tableau de n valeurs régulièrement espacées entre a et b (bornes incluses).
np.cumsum(x)
Renvoie un tableau où le terme d’indice i est la somme x[0] + x[1] + … + x[i].
Un exercice pour vérifier ta maîtrise
On souhaite conjecturer graphiquement le nombre de solutions de l’équation \[ \mathrm{e}^{-x}+x = \frac{2}{x+1}\] Compléter le programme suivant pour qu’il affiche la représentation graphique sur \( [0,3] \) des fonctions \( f: x \mapsto \mathrm{e}^{-x}+x \) et \( x \mapsto \frac{2}{x+1} \) dans un même repère.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.exp(-x) + x
x = np.linspace(0, 3, 200)
y = f(x)
z = 2/(x+1)
plt.plot(x, y)
plt.plot(x, z)
plt.grid()
plt.show()Le tableau x contient 200 valeurs régulièrement espacées entre 0 et 3
Comme on veut que plt.plot(x,y) renvoie la représentation graphique de \( f \) sur \( [0,3] \), on pose donc y = f(x)
L'instruction z = 2/(x+1) stocke dans z les images des coefficients de x donc, comme on veut représenter graphiquement la fonction \( x \mapsto \frac{2}{x+1} \), on complète le second plot en plt.plot(x,z)
Le graphe obtenu permet de conjecturer que l'équation \( f(x) = \frac{2}{x+1} \) admet une unique solution.
Et pour quelques minutes de plus…
Prendre en main la programmation, pas à pas.
Ces exercices sont conçus pour t’aider à maîtriser progressivement la programmation en Python, en partant de la lecture et de la compréhension du code, jusqu’à l’écriture autonome de scripts complets.
L’objectif n’est pas d’aller vite, mais de construire des automatismes solides, en comprenant ce que fait chaque instruction, puis en apprenant à les utiliser par toi-même.
L’ordre des exercices est volontaire : on lit, on comprend, on complète, puis on écrit seul. Prends le temps de chaque étape : c’est la clé pour progresser durablement.
Niveau 1 Analyser un code
Comprendre avant d’écrire.
Dans cette première série, tu observes et analyses des scripts Python déjà écrits.
L’objectif est de comprendre la logique du programme, le rôle des variables, des boucles
et des conditions, et d’être capable de prévoir ce que le code affiche ou calcule.
Niveau 2 Compléter un code
Écrire, mais avec un cadre.
Ici, tu passes à l’écriture sans partir de zéro.
Le squelette du programme est fourni : il te reste à compléter certaines instructions
pour que le code fonctionne correctement.
Ce format permet de se concentrer sur l’essentiel, sans se perdre dans la structure générale.
Niveau 3 Écrire un code complet
Passer à l’autonomie.
Dans cette dernière série, tu écris un programme complet à partir d’une consigne.
Tu dois organiser ton code, choisir les bonnes instructions et construire la logique globale du script.
C’est ici que tu mets en pratique tout ce que tu as appris dans les niveaux précédents.
Contenu réservé aux membres
Il faut être membre et connecté pour accéder aux exercices et aux corrigés.
