Déroulement pratique de l’épreuve oral de mathématiques

Avant toute chose, pour bien se préparer à l’oral il est préférable de savoir comment il se déroule ! À HEC comme à l’ESCP, l’épreuve orale de mathématiques se déroule en deux temps : la préparation, puis le passage devant un jury de deux examinateurs.

Le candidat dispose de 30 minutes de préparation pour traiter l’exercice qu’il présentera. Le temps de passage, de 30 minutes également, est décomposé en deux temps :

• la présentation de l’exercice préparé, pendant 20 à 25 minutes ; cet exercice porte sur l’un des trois grands thèmes du programme (algèbre, analyse ou probabilités), l’exercice proposé à HEC débutant toujours par une question de cours (énoncé une définition, un théorème ou des propriétés du cours) en rapport avec l’exercice,
• la résolution d’un exercice non préparé, pendant 5 à 10 minutes ; cet exercice portera toujours sur un thème différent de l’exercice préparé.

Dans tous les cas, le sujet comporte un exercice de probabilités ou d’informatique, que ce soit l’exercice préparé ou non, l’autre portant sur l’algèbre ou l’analyse.

Il est également important de se souvenir que :

• en maths appliquées, tous les sujets comportent de l’informatique,
• en maths approfondies, près de 75% des sujets comportent de l’informatique,
• en maths appliquées comme en maths approfondies, de plus en plus de sujets demandent des représentations graphiques ou des analyses de graphique.

Conseils pour préparer l’épreuve orale

Après deux années de préparation, il ne faut pas croire que les quelques jours qui s’écoulent entre les résultats d’admissibilité et l’oral vont révolutionner ton niveau. L’oral se prépare surtout au cours les deux années de classe préparatoire, en apprenant et comprenant le cours, en travaillant les méthodes de raisonnement fondamentales et en s’entraînant régulièrement, de manière intensive.

Cependant, le temps de préparation entre les écrits et les oraux est aussi capital, mais doit s’organiser différemment. Car si le cours et les méthodes fondamentales sont maîtrisées, l’exercice de l’oral est très différent de l’écrit. Durant cette période, je te recommande donc de faire le plus d’exercices possibles dans les conditions de l’oral, c’est-à-dire :

• accorder 30 minutes de préparation minimum avant de regarder la correction (ou même les indications),
• organiser tes notes pour qu’elles soient utiles à l’oral, et notamment pour que tu sois capable d’identifier rapidement où sont les différentes questions,
• réfléchir à ce qui mérite d’être dit, et ce qui ne nécessite pas de détail (quels calculs, par exemple, devront être conduits au tableau),
• rédiger systématiquement les résultats du cours utilisés avec leurs hypothèses.

Ce travail devra être accompagné par un travail approfondi de l’informatique ainsi qu’une reprise systématique du cours. “ Le jury de mathématiques recommande avec insistance aux futurs candidats une très solide assimilation du cours et il rappelle sa préférence pour le raisonnement plutôt que pour la récitation de formules mal assimilées”.

À titre d’exemples, voici une liste de points relevés par les jurys de l’oral HEC dans un lointain rapport de jury, mais qui a encore toute sa pertinence :

Si cela n’a pas été fait pendant l’année, cette période de révision est aussi l’occasion de prendre de bonnes habitudes de réflexion et de contrôle des résultats :

• être capable d’identifier un résultat manifestement faux, comme une variance négative, une probabilité négative ou supérieure à 1, somme des probabilités d’un système complet d’événements différente de 1, inverse d’une matrice ayant une ligne ou une colonne nulle..
• être capable de vérifier qu’un résultat est vraisemblable, en étudiant des cas particuliers par exemple,
• prendre l’initiative de prendre un exemple, un cas particulier, ou de faire un schéma pour réfléchir à une question non résolue (par exemple au cours de l’exercice sans préparation) ; dans cette perspective, il est donc important d’être capable rapidement de représenter les termes d’une suite vérifiant une relation du type u_{n+1}=f(u_n), une densité ou la fonction de répartition des lois usuelles, d’interpréter graphiquement la convexité ou la concavité d’une fonctiondots

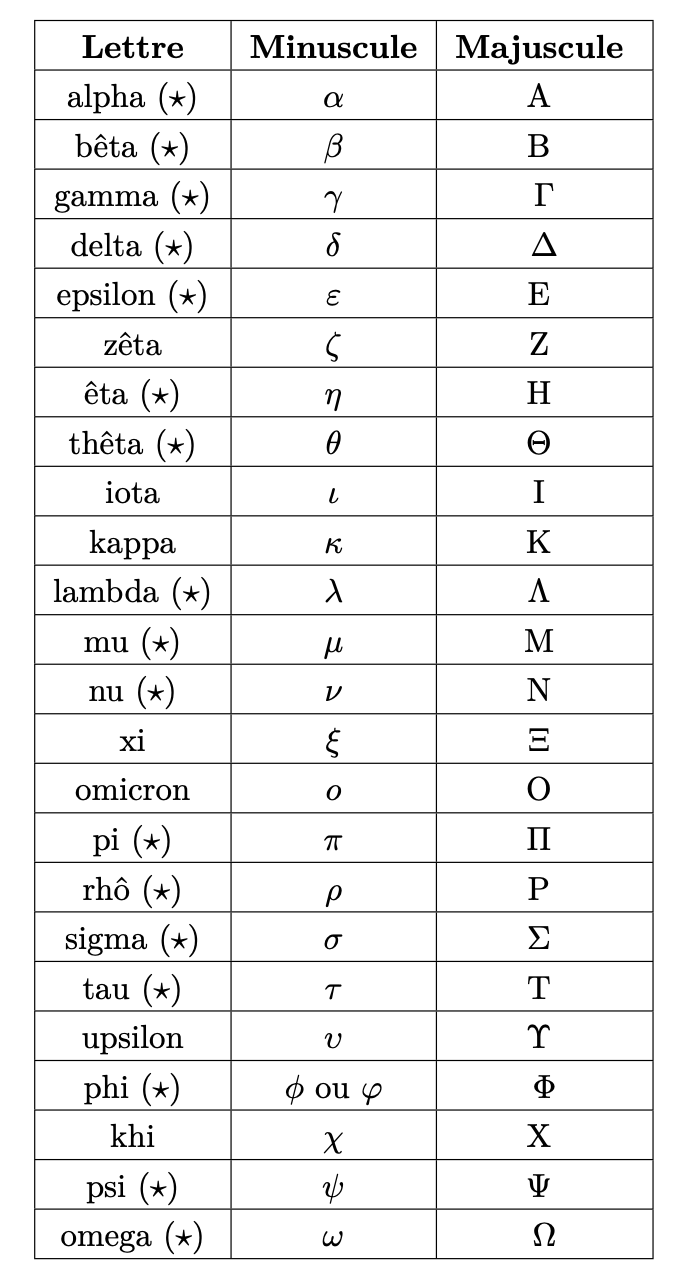
Enfin, il ne peut pas faire de mal de connaître les lettres de l’alphabet grec couramment utilisées en mathématiques : si cela n’a pas d’impact direct sur la notation, que peut penser un jury d’un candidat admissible à l’oral d’HEC ou de l’ESCP qui lirait “alpha” la lettre “lambda” ? Il s’agit d’un rapport curieux au savoir pour un candidat aspirant à intégrer une grande école !

Voici donc, en exclusivité, l’alphabet grec (les lettres figurant dans le bagage minimal étant signalées par une étoile) :